TABLAS SEMÁNTICAS O ÁRBOLES LÓGICOS
TABLAS SEMÁNTICAS O ÁRBOLES LÓGICOS
Las tablas semánticas:
Hemos visto que las deducciones pueden hacerse atendiendo a los problemas
de derivación, realizándose esta última a través
de la aplicación de las reglas básicas o derivadas.
Pero también podemos utilizar otro criterio: el semántico,
según el cual, y suponiendo que la deducción sea correcta,
no podemos obtener una conclusión falsa de premisas verdaderas.
La semántica atiende por una parte al hecho al que se refiere la
proposición y, por otra parte, a su valor de verdad.
El método de las tablas semánticas supone una búsqueda de contraejemplos que invaliden el argumento. Es una especie de reducción al absurdo, en la que se supone la verdad de la negación de la conclusión y, a partir de ella, se llega a una contradicción. Veámoslo.
REGLAS SEMÁNTICAS
La búsqueda de contraejemplos que invaliden la argumentación se realiza a través de la aplicación de una serie de reglas que tienen bastante parecido con las reglas básicas del cálculo de juntores.
Estas reglas son las siguientes:
- Regla de negación:
Doble negación (DN)
Siempre que tengamos una doble negación podemos inferir la afirmación de dicho término:
- Reglas de la implicación:
verdad de la implicación (VI):
Siempre que se nos de una implicación podremos afirmar separadamente que su antecedente es falso o su consecuente es verdadero:
 |
La barra vertical que separa a ¬A de B implica la existencia de una bifurcación en la derivación, puesto que pueden darse varias posibilidades de las cuales, al menos una, ha de ser verdadera (o
Falsedad de la implicación (FI)
Una implicación es falsa cuando su antecedente es verdadero y su consecuente falso:
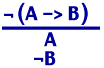 |